학습(Learning) & 손실함수(Loss function) & 역전파(Backpropagation)
Ⅰ. 학습(Learning)이란?
- Training data로부터 weight 매개변수의 최적값을 자동으로 획득하는 것을 의미합니다.
- 신경망이 학습할 수 있도록 해주는 지표가 손실 함수(Loss function)이며, 손실 함수의 출력이 최소가 되도록 하는 weight 매개변수를 찾는 것이 학습의 목표이고요.
+ 손실 함수에 대해서는 아래에서 설명합니다.
Ⅱ. 손실 함수(Loss function)이란?
- 신경망 성능의 좋고, 나쁨을 나타내는 성능 지표입니다.
+ 손실 함수의 값을 가능한 최소화하는 매개변수를 찾기 위해, 매개변수의 미분(=기울기, gradient)을 계산하고, 미분 값을 근거로 하여 매개변수의 값을 서서히 갱신하는 과정을 반복하게 됩니다.
+ “Weight 매개변수의 손실 함수의 미분" → weight 값을 변화시켰을 떄손실 함수의 값이 어떻게 변하는가
ⅰ. 손실함수의 계산
- 일반적으로 평균 제곱 오차(Mean Squared error, MSE)와 교차 엔트로피 오차 (Cross Entropy error, CEE)를 사용합니다.

+ CEE의 경우, 정답에 해당되는 출력이 커질수록 0에 가까워지고, 출력이 1일 때는 0이 됨. 반대로 정답일 때의 출력이 작아질수록 오차는 커지는 특징이 있습니다.
- 앞서 말씀드렸듯이, 훈련 데이터에 대한 함수의 값을 구하고, 그 값을 최대한 줄여주는 weight 매개변수를 찾는 것이 목표입니다.
+ 그 말은 즉, 모든 훈련 데이터에 대해서 손실 함숫값을 계산하여야 한다는 것입니다.

- 위는 평균 손실 함수를 구한 것이며, 전체 데이터에 대해서 평균 손실 함수를 계산 가능합니다.
+ 그러나 100100만 개의 데이터가 있다면? à 평균 손실 함수를 계산하는 것은 매우 비효율적입니다.
+ 그해서 전체 훈련 데이터에서 일부를 랜덤으로 골라 학습을 수행하며, 골라낸 일부를 batch batch라고 합니다.
Ⅲ. 기울기(Gradient)
- 역전파(Backpropagation)를 설명드리기 전에, 해당 개념을 먼저 이해할 필요가 있어서 설명드리겠습니다.
- 신경망에서는 미분(=기울기, gradient)을 계산하여야 하여야 합니다.
+ 이때 “기울기”의 의미는 weight 매개변수에 대한 손실 함수의 기울기를 의미합니다.
→ 즉, weight를 변경하였을 때, 손실 함수의 값이 얼마나 변하느냐를 계산한다는 것입니다.
+ 2x3 W( weight matrix)와 손실함수 L가 있다고 할 때, 아래와 같이 표현이 될 것입니다.

- 계산된 기울기는 다음에 나오는 경사법(Gradient method)을 이용하여서 weight 값을 경신하면 됩니다.
+ 1번만 갱신하는 것이 아니라, 여러 번 갱신하면서 손실 함수의 값이 가능한 최소가 되도록 합니다.
Ⅳ. Gradient decent(경사 하강법)
- 미분(=기울기 gradient)을 잘 이용해, 함수의 최솟값(혹은 가능한 작은 값)을 찾는 것이 경사 하강법의 목표입니다.
- 현 위치에서 기울어진 방향으로 일정 거리만큼 이동 이동한 곳에서 기울기를 계산하고, 기울어진 방향으로 다시 나아가는 것을 반복하면서 함수의 값을 점차 줄이는 것을 경사법(gradient method)이라 합니다.
+ 딥러닝을 공부하고 계신 분들이 라면, 많이들 들어보신 내용일 것입니다.
- 수식은 아래와 같이 될 수 있습니다.
+ η (eta)는 학습률(learning rate)을 나타내며, 너무 크면 발산, 너무 작으면 갱신이 거의 진행되지 않는 문제가 있습니다.

- 아래의 그림은 iteration을 하면서 최소가 되는 gradient를 찾아가는 모습을 잘 나타내어 가지고 왔습니다.
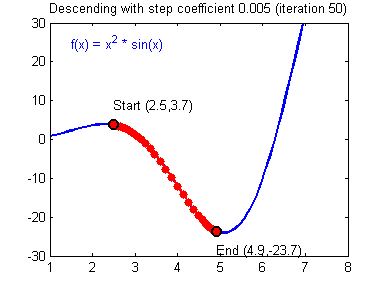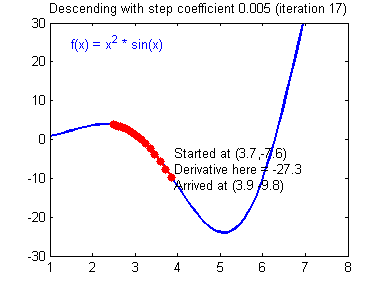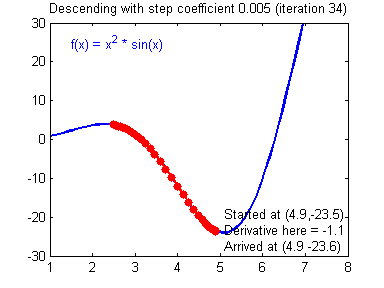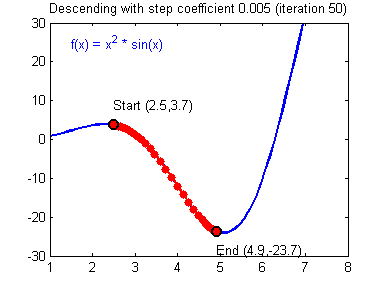
이제부터 역전파(backpropagation)에 대해서 이야기해볼 수 있을 것 같습니다. 위에 내용이 이해 안 가신다면, 다시 한번 읽어보신 다음, 다음으로 넘어가시는 걸 추천드립니다.
Ⅴ. Backpropagation
- Backpropagation의 원래 의미는 “Backward propagation of errors" 오차를 역으로 전파”하는 뜻입니다.
- Backpropagation은 weight 매개변수의 기울기를 효율적으로 계산하는 방법이며, Backpropagation 계산 과정을 이해하기 위해서는 연쇄 법칙(chain rule)을 이해하는 것이 필요합니다.
- 예를 들어 보겠습니다.
+ z=(x+y)^2의 식이 있다고 가정
+"x+y"를 "t"로 치환한다면, 위의 식은 z=t^2으로 다시 표현 가능합니다.

+ "z=(x+y)^2"를 그림 형태로 나타낸다면 아래와 같이 표현 가능할 것입니다.

> Backpropagation 의 순서는 아래와 같이 진행됩니다.
① 오른쪽에서 왼쪽으로 신호를 전파
② 해당 node의 입력 값을 그대로 사용
③ 해당 node의 Forward propagation 에서의 입력에 따른 출력에 대한 미분을 사용
④ ②과 ③의 곱셈한 값을 다음 node로 전파
위의 개념을 숙지하셨다면, 이제부터는 각 , layer 혹은 활성화 함수는 어떻게 역전파가 되는지 알아보겠습니다.
ⅰ. Affine 계층
- Matrix 간 dot 연산
+ Forward propagation 기준 node 입력 input value와 weight 값이 반대로 전달시킨 다음 Backpropagation의 입력을 곱한 것이 Backpropagation의 출력이 됨
-Matrix 간 + 연산
+ Backpropagation의 입력이 그대로 전달

ⅱ. ReLU
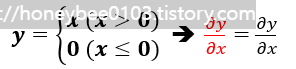
- Forward propagation 기준, x가 0보다 크면 backpropagation 때에는 값을 그대로 전파됩니다.
- Forward propagation 기준, x가 0보다 이하면 backpropagation 때에는 0을 전파됩니다.

ⅲ. Sigmoid

- Forward propagation 기준, 출력 y만으로도 backpropagation 계산이 가능합니다.
+ 좋은 방법이라고 할 수 있습니다.

- 그러나 sigmoid function에는 매우 치명적인 문제점이 존재합니다.
+ Forward 기준 입력 값이 크거나 작게 되면 1과 0으로 수렴하는데, 이는 neuron들의 gradient를 소멸시키게 됩니다.
> 즉 다시 말하면, 수렴된 뉴런의 gradient 값은 0이기 때문에 backpropagation에서 0이 곱해져서, gradient가 kill 된다는 것입니다.
+ 원점 중심이 아님(Not zero-centered) 항상 양수를 출력하기 때문에 출력의 가중치 합이 입력의 가중치 합보다 커질 가능성이 높음( =편향 이동(bias shift) )
> 각 레이어를 지날 때마다 분산이 계속 커져 가장 높은 layer에서는 활성화 함수의 출력이 0이나 1로 수렴하게 되어 gradient vanishing 문제가 일어나게 됩니다.
ⅳ. Softmax-with-Loss function
- Softmax는 학습 시, 가장 마지막 layer에서 사용되며, loss function과 이어집니다.
※참고로 추론(Inference) 시 에는 Softmax의 입력 중 가장 큰 값만 알면 되기 때문에, Softmax를 사용하지 않아도 됩니다.
- Softmax의 backpropagation은 forward propagation 시의 softmax 출력과 정답 레이블(t) 간의 차로 계산해 낼 수 있습니다.
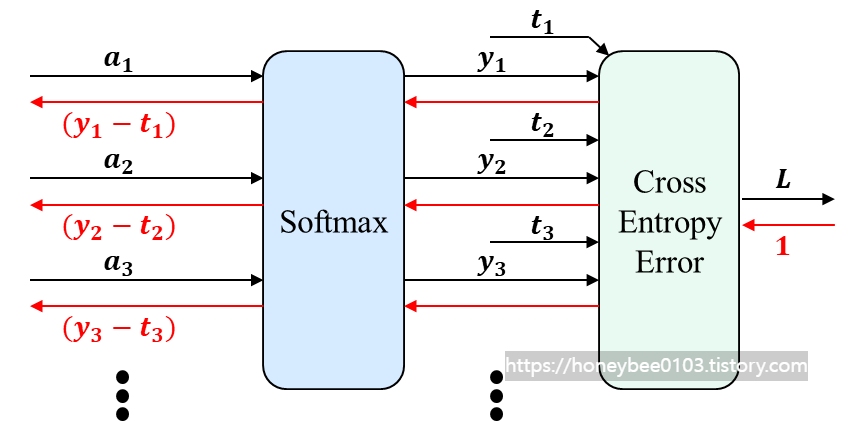
※ 책에서 손실 함수와 함께 역전파 내용을 다루어서, 저도 동일하게 하였으므로 참고 부탁드립니다.
6. 최종 정리
- 역전파(backpropagation)의 계산은 아래와 같이 일반화가 가능합니다.
+ 참고로 Backpropagation은 node의 index는 다르지만, node에서의 수행 동작은 같기 때문에 아래와 같이 일반화가 가능하다는 것을 알아주세요!

- 그리고 Weight 업데이트 수식은 아래와 같이 정의 가능합니다.

이상 역전파에 대한 내용을 마치겠습니다.