Ⅰ. Epipolar line
- 뒤에 이어서 Essential matrix 와 Fundamenal matrix을 설명하기에 앞서 해당 내용을 추가합니다.
- Epopolar line은 아래와 같은 수식으로 나타낼수 있습니다.

- 또, 다르게는 아래와 같이 풀어 쓸 수 있습니다.

- 이를 종합하여, 다시 식을 써내려가면,

- 위와 같이 수식은 정의될 수 있다.
- 이어서 이전 과정에서 배웠던 수식을 가져와보면, 아래와 같이 된다.
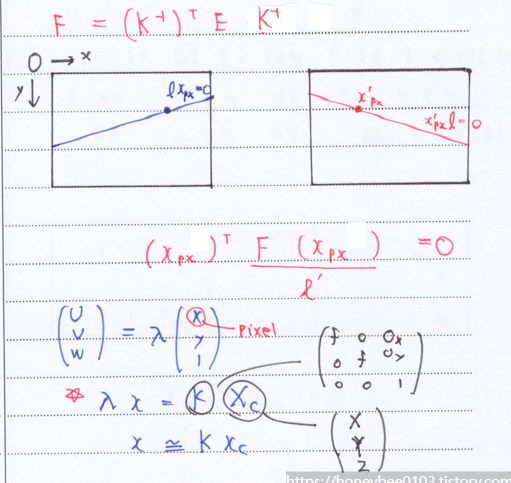
- 정리하면, k(intrinsic parameter)와 Fundamental matrix를 안다면, pixel 좌표를 이용
- 만약 모른다면, Essential matrix와 camera 좌표계를 이용하면 됨
- 위의 내용을 잘 이해 못해도, 아래의 내용을 계속 보면 이해가 될 것이다.
Ⅱ. Essential matrix
- Essential matrix의 정의는 아래와 같이 정의 될 수 있음
+ 3D 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p'에 투영됐다고 하면 두 영상 좌표 p와 p' 사이에는 다음 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심
+ 임의의 두 지점에서 찍은 영상의 매칭점들을 항상 관계지을 수 있으며, 3×3 행렬 E를 Essential Matrix라 함
(※ 인용 사이트 : https://darkpgmr.tistory.com/83) ← (정말 정리를 잘한신것 같음)
- 이전에 그렸던 그림을 다시 보게되면 image plane에 맺힌 두점 x와 x' 의 관계는 아래의 수식처럼 정의가 가능함
+ Rotation 시키고 translation 시키면 되니까요

- 위의 수식을 기반으로 다시 식을 풀어내면 아래와 같이 됩니다.
+ 휘어진 "Τ"는 Cross product를 나타내며, 자기 자신에 대한 cross product는 zero이지요?
+ 하나의 x'에 위의 수식을 대입하게되면 T는 Cross product로 zero가 되어 최종적으로는 x'TRx 가 남게되고, TR을 E로 치환합니다.
+ 최종적으로 E가 우리가 찾는 Essential matrix입니다.

Ⅲ. Fundamental matrix
- Fundamental matrix의 정의는 아래와 같이 정의 될 수 있음
- Essential Matrix는 카메라 내부 파라미터 행렬인 K가 제거된 좌표계에서의 변환관계 임
- Fundamental matrix는 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀(pixel) 좌표 사이의 기하학적 관계
(※ 인용 사이트 : https://darkpgmr.tistory.com/83)
ⅰ. Fundamental matrix 추정 → Eight point algorithm
- Fundamental matrix는 8의 장도를 가지며, 각 point 일치점은 linear equation 으로 나타내어질 수 있음

- 다시 위의 행렬을 풀어 쓰면, 아래와 같이 됨

- 즉, 'F' Fundamental matrix 값을 알면, image plane에 매칭되는 point를 바로 알 수 있으며, 'E' Essential matrix를 바로 알 수 있음
+ 'E' Essential matrix 를 알고 있다면, R과 T를 바로 알 수 있음
> 그러면 CCD 상에 맺히는 Point만 알면, 다른 CCD상에 매칭되는 Point를 알 수 있음

- 우측 수식은 Ⅰ장에서 정리한 수식인 것을 알 수 있다.
- 최종적으로 Fundamental matrix와 Essential matrix 그리고 좌표계가 어떻게 연관되는지 알수 있다,
'영상처리 > Computer vision' 카테고리의 다른 글
| Stereo Matching (0) | 2022.10.03 |
|---|---|
| Depth & Disparity (2) | 2022.10.03 |
| Stereo vision (0) | 2022.10.01 |
| Image processing(3) (0) | 2022.09.26 |
| Image processing(2) (0) | 2022.09.25 |




댓글