CNN(Convolution Neural Network )

이제 영상처리 뿐만 아니라 다른 분야에서도 막대한 영향을 끼친 CNN에 대해서 정리해보고자 합니다.

 

Ⅰ. CNN(Convolution Neural Network)

-  CNN(Convolution Neural Network)는 이미지 인식 분야에서 많이 활용되고 있습니다.
- 이전 포스팅과 달리, 합성곱 계층(Convolution layer)와 풀링 게층(Pooling layer)가 존재합니다.

FCL 과 CNN의 차이

    + 입력된 영상의 정보가 소실되지 않고 전달되는 것이 특징이며, 이는 매우 중요한 특징이니 반드시 기억하세요!
- 이전에 Fully Connected Layer의 문제점은 입력된 영상의 정보가 무시된다는 것입니다.
    + 이미지의 정보를 무시하고, 모든 입력 데이터를 동등한 뉴런(=같은 차원의 뉴런)으로 취급합니다.
        > 예를 들어 보면, EDGE나 TEXTURE는 매우 중요한 특징입니다. 그런데 이를 무시하고 한 픽셀을 단순한 뉴런만으로 취급한다면? EDGE 정보나 TEXTURE 정보가 의미가 없어지겠지요?
- “CONV.” 층의 입출력 데이터를 특징 맵(Feature map)이라고 합니다.
    + 또한, CNN에서는 패딩(Padding), 스트라이드(Stridde) 등의 하이퍼파라미터(hyperparameter)가 존재하는 것을 기억하세요!

 

이제부터 각 layer와 파라미터가 무엇인지에 대해서 정리해보겠습니다.

 

Ⅱ. Convolution 연산

- 딥러닝이나 CNN을 공부해보신 분들은 다 아시겠지만, 커널(혹은 필터)가 입력 영상을 슬라이딩 해나가면서 연산을 수행합니다.
- Convolution 연산은 일반적인 필터 연산 처리와 동일합니다.
    + Fully connected layer에서 weight가 CNN에서는 필터의 내부 값이 weight에 해당된다고 보시면 됩니다.
    + 여기서는 Convolution 연산만 표시되어 있지만, 실제로는 Bias에 대한 계산도 있는 것을 잊지말아주세요!
    + 나중에 설명을 드리겠지만, CNN을 Backpropagation을 수행한다는 것은, 각 필터 내의 값을 조정하면서 손실 함수의 값을 최소화 하도록 한다는 것입니다.
- 아래 그림을 보시면 조금더 쉽게 이해 가실 겁니다.
    + 3*3 필터가 5*5 이미지를 슬라이딩하는 것을 보실 수 있습니다.

 

 

3*3 필터를 5*5 입력 데이터에 적용한 예시, https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

3*3 필터를 5*5 입력 데이터에 적용한 예시, https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

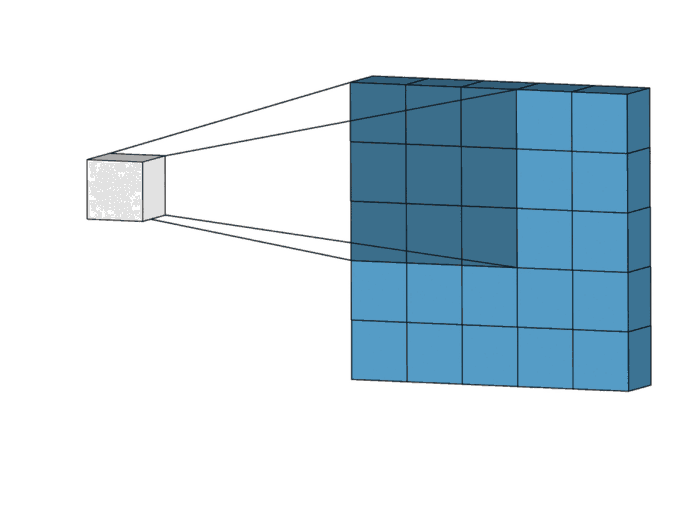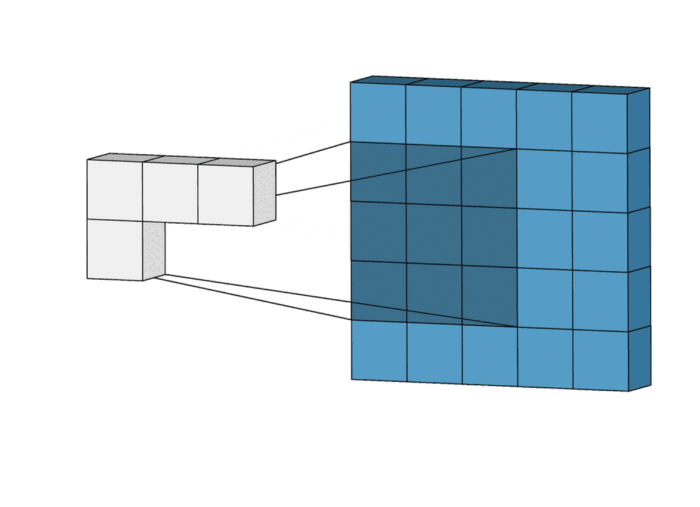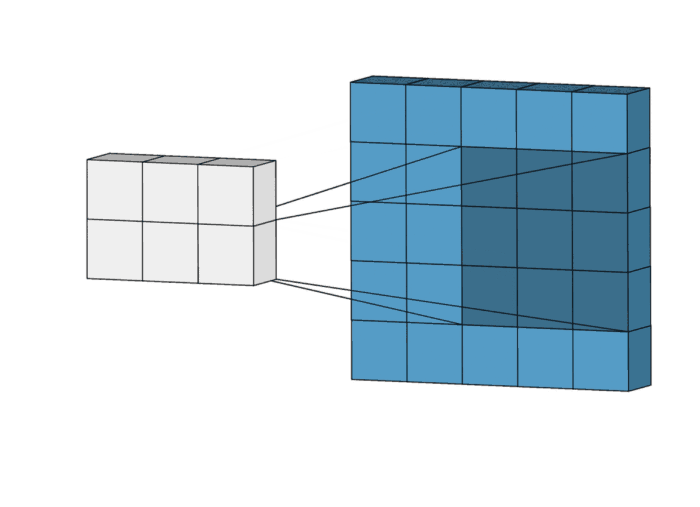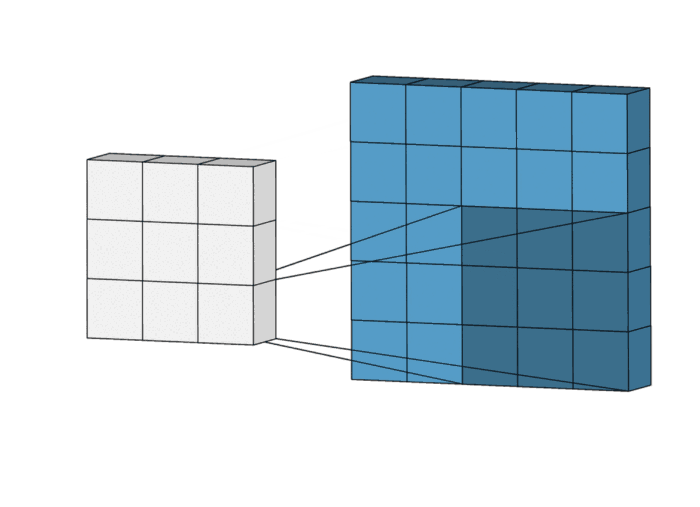
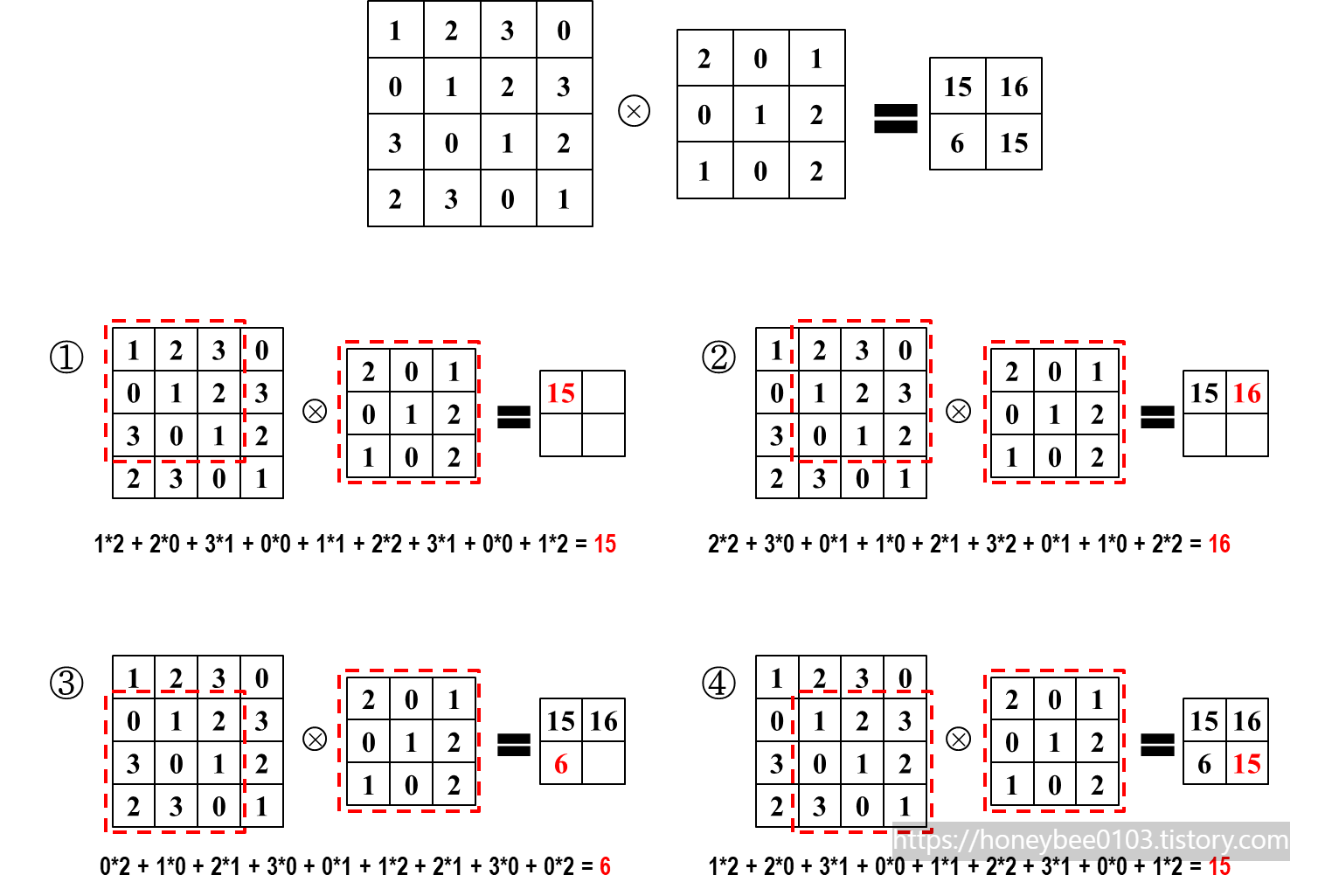
- 저도 예시를 들어 보겠습니다.
    + 아래와 같이 3*3 필터와 4*4 이미지가 있다고 가정합니다.
    + 계산 과정은 아래와 같이 될 것입니다.
    + 눈치채셨겠지만, Convolution의 연산은 MAC(multiply–accumulate) 연산입니다.

Convolution 연산 예시

Ⅲ. 스트라이드(Stride) 및 패딩(padding)

- 패딩과 스트라이드는 Convolution 연산 시 적용되는 파라미터입니다.

- 패딩(padding) : 입력 데이터의 외곽에 특정한 값으로 채우는 것입니다.

    + 패딩을 통해서, 출력 크기를 조절 가능합니다. Layer가 많은 신경망인 경우, layer가 깊어질수록 출력의 크기가 매우 작아지게 되는 경우가 발생할 수 있는데 패딩을 통해서 이러한 사태를 방지 가능하지요.

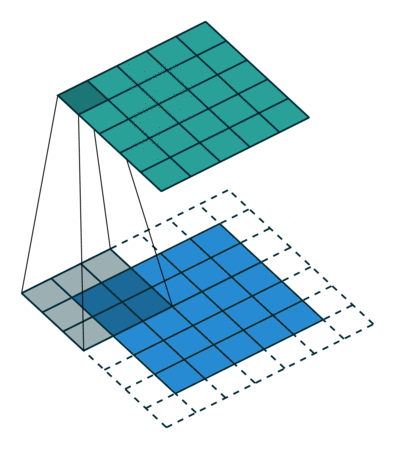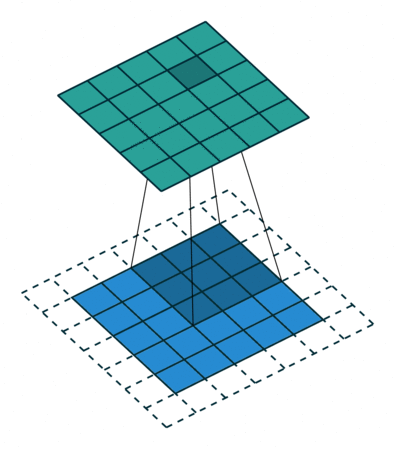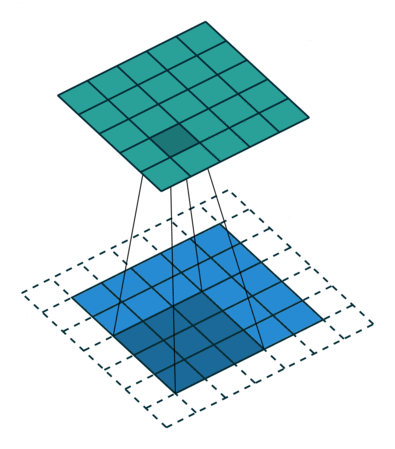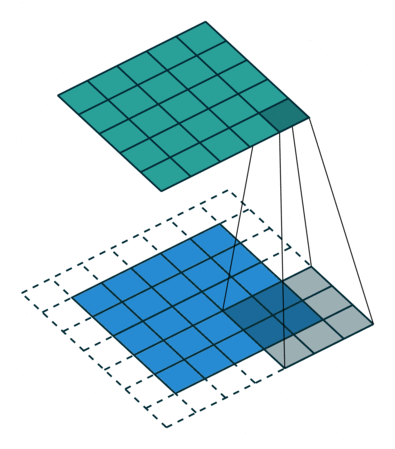
- 스트라이드(Stride) : 필터를 적용하는 위치의 간격을 의미합니다.

    + 연산량을 감소시킬 수 있습니다.

- 아래의 그림을 보시면 바로 이해가 가실겁니다. (말 보다는 그림이 확실히 이해가 가죠?)

 

패딩 1의 예시, https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

스트라이드 2의 예시, https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

- 그렇다면 패딩과 스트라이드도 예시를 들어 보겠습니다.

    + 패딩 1

        > 원래의 이미지에서 1개의 line이 둘러쳐졌습니다.

패딩 1예시

    + 패딩 2

        > 원래의 이미지에서 2개의 line이 둘러쳐졌습니다.

패딩 2 예시

    + 스트라이드 2

        > 필터가 1칸씩 움직이지 않고, 2칸씩 움직입니다.

        > 또한, 그만큼 skip을 하기때문에 연산량이 줄어드는 것입니다.

스트라이드 2 예시

Ⅳ. 3D Convolution

- 이제는 2D 이미지 채널이 1인, 즉 Gray 이미지를 다루었다면 3D 이미지 채널이 3인 Color(예를 들면 RGB 이미지) 이미지 연산이 어떻게 되는지 알아 보겠습니다.

- Color 이미지의 경우, Height*Width*Channel로 구성됩니다.

    + 여기서 아셔야 반드시 숙지하셔야 될 것은 Channel 수와 필터의 수가 같다는 것입니다.

    + 또한, 모든 채널의 필터의 크기는 동일하다는 것입니다.

- 그림의 예를 보시면 바로 아실수 있을 겁니다!

 

https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

 

- 앞의 예를 보셨겠지만, 마지막은 출력은 2D 형태로 나오게 됩니다.

    + 출력 feature map의 크기는 패딩, 스트라이드, 필터 크기, 입력 feature map 크기를 알면 계산할 수 있습니다.

Output feature map의 크기 계산 수식

        > 출력 크기 : (OH, OW)

        > 입력 데이터 크기 : (H, W)

        > 필터 크기 : (FH, FW)

        > Padding : P, Stride : S

 

- 이것도 예를 들어 보겠습니다.

    + CASE1. 입력 (7,7), 필터 (3,3), P=1, S=1

case1 조건 시, output feature map 크기 계산

 

    + CASE2. 입력 (7,7), 필터 (3,3), P=1, S=2

case2 조건 시, output feature map 크기 계산

Ⅴ. 3D OUTPUT 계산, 총 정리

- 3차원 DATA의 표현를 아래와 그림과 큐브 형태로 그릴 수 있습니다.

    + 입력데이터 (C, H, W) / 필터 (C, FH, FW) / 출력데이터 (OH, OW) (※채널, 높이, 너비 순)

    + 입력 데이터의 각 채널과 필터의 각 채널 간 Convolution 연산 후 합산하여 출력합니다.

input feature map 1 개에 대해 출력 Feature map 이 1 장으로 출력

 

i. 이제 필터 set를 늘려서 생각해봅시다.

    + 그러면 아래와 같은 형태로 그릴 수 있습니다.

        > 필터의 갯수가 "FN"개로 늘어난 것이 보이시나요? 이에 따라서 Output feature map의 수도 "FN"개로 늘어 났습니다!

 

필터 set의 증가에 따른 output feature map 채널 증가

 

ii. 이제 input feature map을 늘려서 생각해봅시다

    + 그러면 아래와 같은 형태로 그릴 수 있습니다.

        > input feature map의 수가 "N"개로 늘어남에 따라, Output feature map의 set가 "N"개로 늘어난 것을 보실 수 있습니다.

input feature map의 증가에 따른 output feature map 증가

 

---

이번 포스팅에서는 CNN에 대해서와 CNN이 어떻게 계산이 되는지에 대해서 알아보았습니다.